
本文为 Andrew Ng 深度学习课程第一部分神经网络和深度学习的笔记,对应第四周深层神经网络的相关课程。
Deep L-layer Neural network
主要复习了之前 Logistic Regression 和单隐藏层的神经网络,并推广到多隐藏层,同时也介绍了深层神经网络的一些符号约定,基本遵循了之前的规则,所以这里不再详述。
Forward propagation in a deep network
以 $4$ 层的神经网络为例,我们来推导一下对于单个样本的正向传播过程:
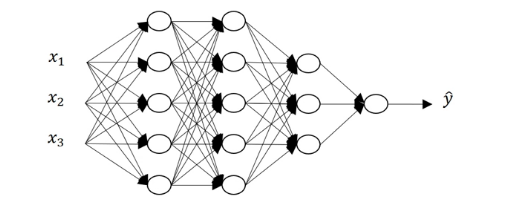
第一层:
推广到第 $l$ 层:
第 $l$ 层向量化版本:
这里有一点需要注意,对于深层神经网络正向传播,它类似一个循环的过程,即从 $1$ to $l$ 的循环,对每一层分别计算正向传播的过程。你可能会想到前面所说的向量化来优化,但这里避免不了显式的 $for$ 循环。
Getting your matrix dimensions right
在实现深层神经网络的过程中,想要降低 bug 的出现概率,你必须非常仔细地检查矩阵维数是否正确。本节就来讨论如何确定矩阵的维数。
以下图的神经网络为例:
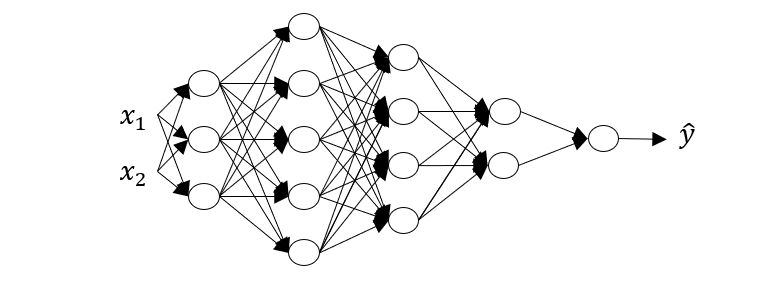
不难看出 $l=5, n^{[0]}=n_x=2, n^{[1]}=3, n^{[2]}=5, n^{[3]}=4, n^{[4]}=2, n^{[5]}=1$,如果我们想要进行正向传播,那么首先需要计算
这里的 $z^{[1]}$ 的维度为 $(n^{[1]},1)$ ,$x$ 的维度为 $(n^{[0]},1)$ ,根据矩阵乘法的规则,可以得到 $w^{[1]}$ 的维度必为 $(n^{[1]},n^{[0]})$ ,同样可以得到 $b^{[1]}$ 的维度为 $(n^{[1]},1)$ 。
总结一下, $W^{[l]}$ 的维度为 $(n^{[l]},n^{[l-1]})$ ,$b^{[1]}$ 的维度为 $(n^{[l]},1)$ 。顺便提一下,$dw^{[l]},db^{[l]}$ 的维度与 $W^{[l]},b^{[l]}$ 相同。
接着,我们需要计算
可以得到,$a^{[l]}$ 的维度与 $z^{[l]}$ 相同,同样为 $(n^{[l]},1)$。
总结一下:
$dw,db$ 的维度与 $W,b$ 相同
接下来,我们看一下向量化后,各矩阵的维数,同样需要计算
我们将 $m$ 个样本横向堆叠,那么 $Z^{[1]}$ 的维度为 $(n^{[1]},m)$ ,$X$ 的维度为 $(n^{[0]},m)$ ,$W^{[1]}$ 的维度为 $(n^{[1]},n^{[0]})$ ,$b^{[1]}$ 的维度为 $(n^{[0]},1)$ ,由于 Broadcasting ,所以实际运算中,会将 $b^{[1]}$ 复制 $m$ 次,形成维度为 $(n^{[0]},m)$ 的矩阵。
在向量化后,各矩阵维度如下:
同样,$dZ,dA$ 与 $Z,A$ 维度一样
Why deep representations
本节从几个例子来探讨了为什么深度神经网络如此强大。
人脸识别
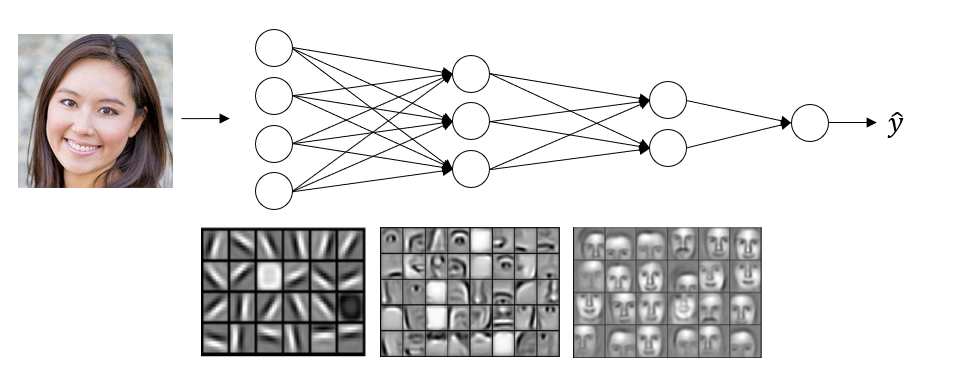
神经网络第一层,你可以把它当成一个边缘探测器 (edge detector) 从原始图片中识别人脸的边缘,下方图片中的一个小方块就是一个隐藏单元,代表着边缘的方向,从而识别边缘。神经网络第二层就将前一层的边缘信息进行组合,组合成面部的不同部分,比如:眼睛,鼻子等等。最后再将这些局部特征放在一起,比如:鼻子,眼睛,下巴,就可以识别整张人脸。可以看出,随着神经网络由浅入深,所获得的信息也是从部分到整体。更深入的部分会在卷积神经网络中讨论。
语音识别
和人脸识别有些相似,也是通过这种从简单到复杂,从部分到整体的方式,在前几层先学习一些简单的特征,再后面几层进行组合,最后去识别更复杂的东西。以语音识别为例,第一层你可能会试着探测一些低层次的音频波形特征,比如:音调,白噪音等等。然后将这些波形组合在一起,就能去探测声音的基本单元,即音位 (phonemes) ,比如 cat 发音的 /k/ /æ/ /t/ 分别为三个音位,有了基本的声音单元后,我们就可以识别单词,从而识别词组,再到整个句子。在前几层学习一些简单的特征,再后面几层进行组合,去识别更复杂的东西。