
本文为 Andrew Ng 深度学习课程第一部分神经网络和深度学习的笔记,对应第三周浅层神经网络的相关课程。
Neural Network Overview
本周,你将学会如何实现神经网络。上周,我们讨论了对数几率回归 (logistic regression) ,并且使用计算图 (computation graph) 的方式了解了梯度下降算法的正向传播和反向传播的两个过程,如下图所示 :
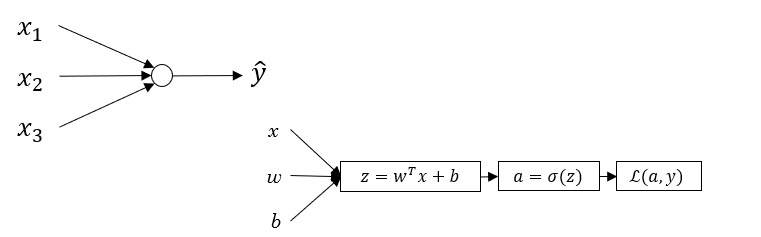
而神经网络 (Neural Network) 是这个样子,如下图 :
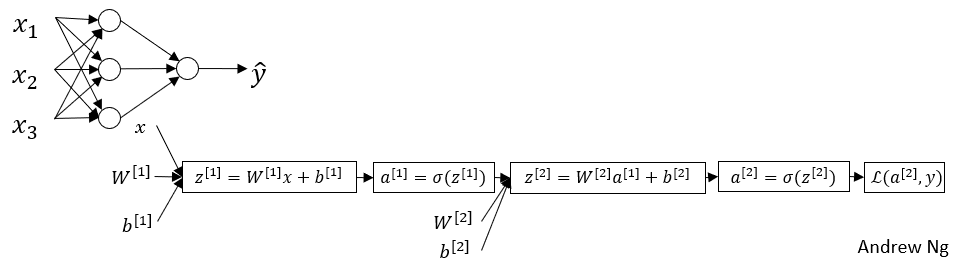
我们可以把很多 sigmoid 单元堆叠起来来构成一个神经网络。在之前所学的对数几率回归中,每一个节点对应着两个计算步骤:首先计算 $z=w^{T}x + b$ ,然后计算 $a=\sigma(z)$ 。在这个神经网络中,三个竖排堆叠的节点就对应着这两部分的计算,那个单独的节点也对应着另一个类似的 $z, a$ 的计算。
在神经网络中,所用的符号也会有些不一样。我们还是用 $x$ 来表示输入特征,用 $W^{[1]}, b^{[1]}$ 来表示参数,这样你就可以计算出 $z^{[1]} = W^{[1]}x + b^{[1]}$ 。这里右上角的 $[1]$ 代表着节点所属的层,你可以认为层数从 $0$ 开始算起,如上图中的 $x_1, x_2, x_3$ 就代表着第 $0$ 层(也称为输入层),三个竖排的节点就属于第 $1$ 层(也称为隐藏层),单独的那个节点属于第 $2$ 层(也称为输出层)。需要注意的是,这与之前用来标注第 $i$ 个训练样本 $(x^{(i)}, y^{(i)})$ 不同,这里用的是方括号。
那么,在这个神经网络模型中,正向传播就分为两层。
- 从输入层到隐藏层:在使用类似对数几率回归的方法计算了 $z^{[1]}$ 之后,再计算 $a^{[1]}=\sigma(z^{[1]})$ 。
- 从隐藏层到输出层:使用相同的方法计算 $z^{[2]}=W^{[2]}a^{[1]}+b^{[2]}$ 。当然,这里的参数 $W^{[2]}, b^{[2]}$ 与 $W^{[1]}, b^{[1]}$ 不同,且第 $1$ 层的输出 $a^{[1]}$ 作为第 $2$ 层的输入 $x$ ,接着同样计算 $a^{[2]}=\sigma(z^{[2]})$ ,得到的 $a^{[2]}$ 就是整个神经网络的输出。
同样,还需要通过反向传播计算 $da^{[2]}, dz^{[2]}$ 等等,这些将会在后面详细讨论。
One hidden layer Neural Network
下图是一张单隐藏层的神经网络,也称为双层神经网络 (2 layer NN) 。我们把最左边的 $x1, x2, x3$ 称为输入层 (Input Layer) ,中间称为隐藏层 (Hidden Layer) ,最右边只有一个节点的称为输出层 (Output Layer) ,负责输出预测值 $\hat{y}$ 。在计算神经网络的层数时,不算入输入层。
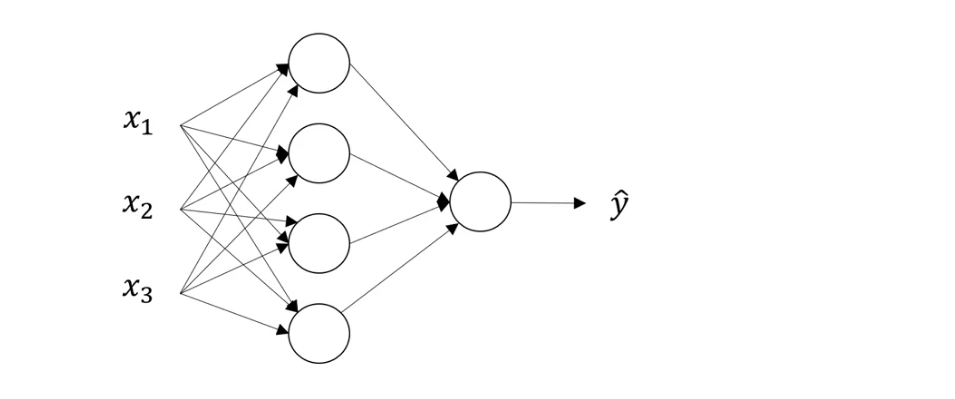
由于在训练过程中,我们看不到这些中间节点的真正数值,不像输入,输出层那样,所以称为隐藏层。
之前,我们用 $x$ 来表示输入,其实它还有一种表示方式 $a^{[0]}$ ,这个 $a$ 有 activation (激活) 的意思,意味这它把不同层的值传递给下一层,起到了激活的作用。用上标 $[i]$ 表示在第 $i$ 层,用下标 $j$ 表示这层中第 $j$ 个节点,如 $a^{[1]}_{2}$ 即表示第 $1$ 层的第 $2$ 个节点。那么上图中隐藏层的4个节点可以写成矩阵的形式:
Computing a Neural Network’s Output
接下来,我们来看神经网络的输出是如何计算出来的。我们可以把神经网络的计算看作对数几率回归的多次重复计算。
我们先来回顾一下对数几率回归的计算过程,如下图:
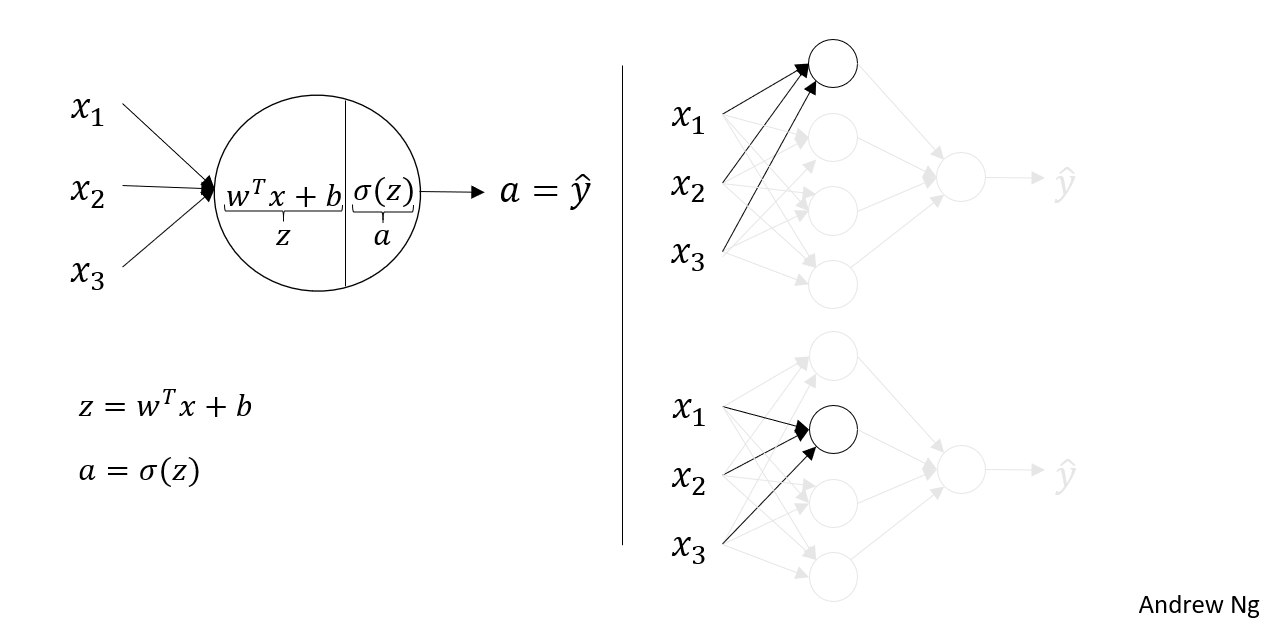
这里的圆圈代表了,对数几率回归的两个步骤。我们先隐去其他节点,如右图,那么它就和对数几率回归非常相似,我们可以计算出 $z^{[1]}_{1} = w^{[1]T}_{1}x+b^{[1]}_{1}$ , $a^{[1]}_{1} = \sigma(z^{[1]}_{1})$ ,上标代表层数,下标表示这层上的第几个节点。
以此类推,我们可以写出:
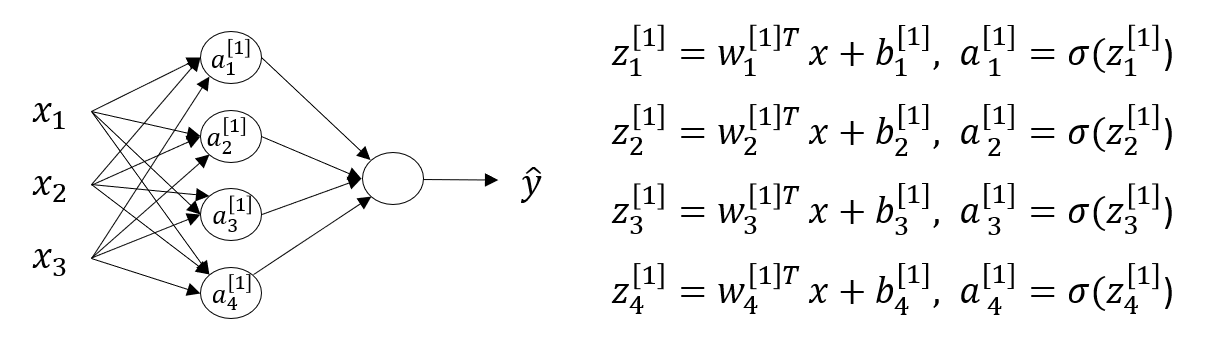
回想起之前所讲的向量化,如果我们想让程序高效的运行,就必须将其向量化。
我们首先先将 $w$ 向量化,由于有4个对数几率回归单元,而每一个回归单元都有其对应的参数向量 $w$ ,且每一个回归单元都有输入 $x_1, x_2, x_3$ ,所以我们可以得到:
那么,我们可以得到如下式子:
在本神经网络中,你就应该计算 (为了更好理解,右下角标注了矩阵的形状) :
记得我们之前说过,可以用 $a^{[0]}$表示 $x$ ,所以 $z^{[1]}$ 有可以写成 $z^{[1]} = W^{[1]}a^{[0]}+ b^{[1]}$ ,那么可以用同样的方法推导出:
所以在代码中,我们只需实现上述的4行代码。然而这是对单个样本的,即对于输入的特征向量 $x$ ,可以计算出 $\hat{y} = a^{[2]}$ ,对于整个训练集的向量化将在接下来的部分介绍。
Vectorizing across multiple examples
接下来,我们实现对整个训练集的向量化。假设你有 $m$ 个训练样本,理解了上述理论,那么我们可以通过输入 $x^{(i)}$ 计算得出 $ \hat{y}^{(i)} = a^{[2](i)}$ 其中 $i \in [1,m]$ 。
还记得我们之前把输入的特征向量 $x^{(1)}, x^{(2)}, …, x^{(m)}$ 横向堆叠起来,得到了一个 $(n_x \times m)$ 的矩阵 $X$ ,即
同样的,我们把 $x^{(1)}, x^{(2)}, …, x^{(m)}$ 横向堆叠起来,那么我们需要计算的式子变为:
其中,$Z^{[1]}$ 的形状为 $(4 \times m)$ ,你可以这样理解,每一个样本对应着矩阵的一列,所以有 $m$ 列,隐藏层中的每一个节点对应着矩阵的一行,所以 $Z^{[1]}$ 有 $4$ 行,规律同样适用于 $X, A$。
Activation functions
到目前为止,我们一直选择 sigmoid 函数作为 activation function (激活函数) ,但有时使用其他函数效果要好得多,它们各自有不同的特点,下面我们来介绍几个不同的激活函数 $g(x)$:
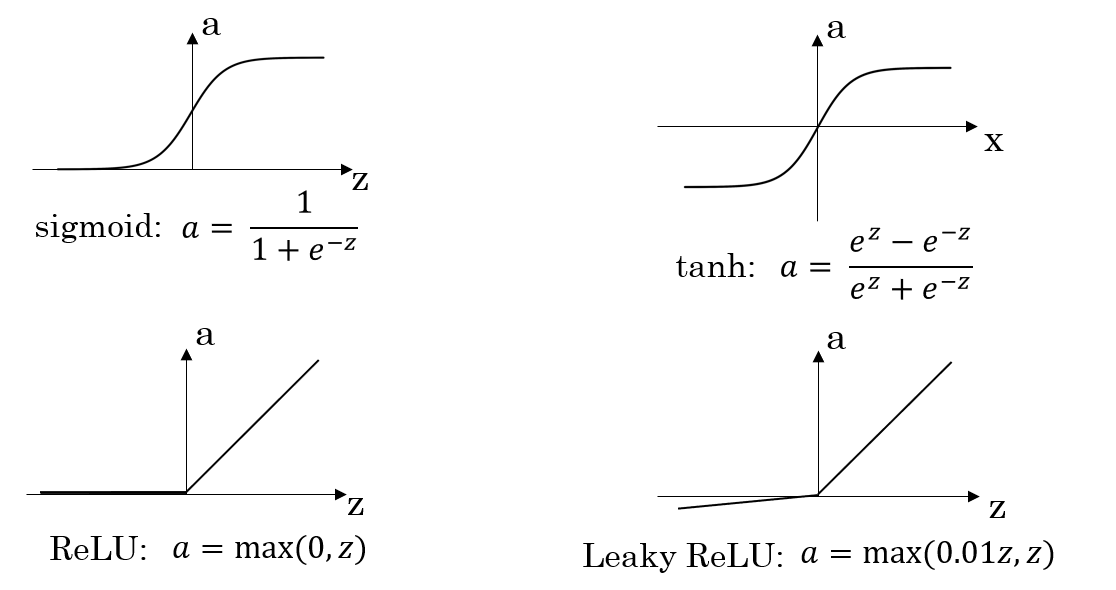
- tanh (双曲正切函数),实际上是 sigmoid 函数向下平移后再经过拉伸得到的。对于隐藏单元,如果你选择 tanh 作为激活函数,它的表现几乎总是比 sigmoid 函数要好,因为 tanh 函数的输出介于 $(-1,1)$ 之间,激活函数的平均值更接近于 $0$ ,而不是 $0.5$ ,这让下一层的学习更方便一点。所以之后我们几乎不再使用 sigmoid 作为激活函数了,但有一个例外,即选择输出层的激活函数的时候,因为二分类问题的输出为 $\{0,1\}$ ,你更希望 $\hat{y}$ 介于 $0,1$ 之间,所以一般会选择 sigmoid 函数。
- 所以之前所举的例子中,你可以使用 tanh 函数作为隐藏层的激活函数,而选择 sigmoid 函数作为输出层的激活函数。同样的,可以使用上标来表示每一层的激活函数,如:$g^{[1]}(x) = tanh(z), g^{[2]} = \sigma(z)$
- 然而,不管是 tanh 还是 sigmoid 函数,都有一个缺点,如果 $z$ 特别大或者特别小,那么在这一点的函数导数会很小,因此会拖慢梯度下降算法。为了弥补这个缺点,就出现了 ReLU (rectified linear unit) 函数,该函数有如下特点:当 $z$ 为正,导数为 $1$,当 $z$ 为负,导数为 $0$ ,当 $z$ 为 $0$ 时,导数不存在,但在实际使用中, $z$ 几乎不会等于 $0$ ,当然你可以在程序中直接把在 $z=0$ 点的导数赋为 $0$ 或 $1$ 。
- 但 ReLU 也有一个缺点,当 $z$ 为负时,导数恒等于 $0$ 。所以就有了 Leaky ReLU 函数,通常表现比 ReLU 函数更好,但实际使用中频率没那么高。
- ReLU 和 Leaky ReLU 的优势在于,对于 $z$ 的许多取值,激活函数的导数和 $0$ 差的很远,这也就意味着,在实践中你的神经网络的学习速度会快很多。
- 总结一下,在我们一般选择 sigmoid 作为输出层的激活函数,而选择 ReLU 作为其他层的激活函数,ReLU 如今被人们广泛使用。