Basic of Neural Networks-1

本文为 Andrew Ng 深度学习课程第一部分神经网络和深度学习的笔记，对应第二周神经网络基础的相关课程。

Binary Classification

在二分分类问题中，目标是训练出一个分类器，以特征向量x (feature vector)为输入，以y (output label)为输出，y一般只有 ${0,1}​$ 两个离散值。以图像识别问题为例，判断图片中是否由猫存在，0代表noncat，1代表cat

通常，我们用 $(x,y)​$ 来表示一个单独的样本，其中x(feature vector)是$n_x​$维的向量 ( $n_x​$ 为样本特征个数，即决定输出的因素) ，y(output label)为输出，取值为 $y\in\{0,1\}​$

则m个训练样本 (training example) 可表示为

$$\{(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),...,(x^{(m)},y^{(m)})\}$$

用$ m=m_{train} $表示训练样本的个数

最后，我们可以用更紧凑的符号 $X$ 表示整个训练集，$X$ 由训练集中的 $x^{(1)}$，$x^{(2)}$，…，$x^{(m)}$ 作为列向量组成，$X\in{\Bbb R}^{n_x*m}$，即 X.shape = $(n_x,m)$

$$\mathbf{X} = \left( \begin{array}{c} \vdots & \vdots & \ldots & \vdots \\\\ x^{(1)} & x^{(2)} & \ldots & x^{(m)} \\\\ \vdots & \vdots & \ldots & \vdots \end{array} \right)$$

同时，把y也放入列中，用 $Y$ 来表示，$Y\in{\Bbb R}^{1*m}$，即 Y.shape = $(1,m)​$

$$\mathbf{Y} = \left( \begin{array}{c} y^{(1)} & y^{(2)} & \ldots & y^{(m)} \ \end{array} \right)$$

Logistic Regression

参照了周志华的西瓜书，把 Logisitic Regression 翻译为对数纪律回归，简称为对率回归。对数几率回归是一种解决二分分类问题的机器学习方法，用于预测某种实物的可能性。

Given x, you want $\hat{y} = P(y=1 \mid x)​$.

In other words, if x is a picture, as talked about above, you want $\hat{y}​$ to tell you the chance that there is a cat in the picture.

根据输入 $x$ 和参数 $w, b$，计算出 $\hat{y}$ ，下面介绍了两种方法 :

Parameter : $w\in{\Bbb R}^{n_x}, b\in{\Bbb R}​$
Output : $\hat{y}​$

One way : $\hat{y} = w^{T}x + b​$ (Linear regression)

• Not good for binary classification
• Because you want $\hat{y}​$ to be the chance that $y​$ equals to one. In this situation $\hat{y}​$ can be much bigger than 1 or negative.

The other way : $\hat{y} = \sigma(w^{T}x + b)$ (Logistic Regression)

• $\sigma(z) = \frac{1}{1+e^{-z}} ​$
• 通过$\sigma(z)$函数，可以将输出限定在$[0,1]$之间

Logistic Regression Cost Function

给出$\{(x^{(1)},y^{(1)})…,(x^{(m)},y^{(m)})\}​$，希望通过训练集，找到参数 $w, b​$ 使得 $\hat{y}^{(i)} \approx y^{(i)}​$ 。所以，我们需要定义一个loss function，通过这个loss function来衡量你的预测输出值 $\hat{y}​$ 与 $y​$ 的实际值由多接近

对于m个训练样本，我们通常用上标 $(i)​$ 来指明数据与第 $i​$ 个样本有关。

通常，我们这样定义Loss function (损失函数) :

$$L(\hat{y},y) = \frac{1}{2}(\hat{y} - y)^2$$

但在对数几率回归中一般不使用，因为它是non-convex (非凸的) ，将来使用梯度下降算法 (Gradient Descent)时无法找到全局最优值

在对数几率回归中，我们使用的损失函数为 :

$$L(\hat{y},y) = -(y \log\hat{y} + (1-y) \log(1-\hat{y}))$$

If y = 1 : $L(\hat{y},y) = -\log(\hat{y})​$, you want $\hat{y}​$ to be large

if y = 0 : $L(\hat{y},y) = -\log(1-\hat{y})​$, you want $\hat{y}​$ to be small

所以，这个损失函数和 $L(\hat{y},y) = \frac{1}{2}(\hat{y} - y)^2$ 类似，都希望 $L$ 越小越好

上述的Loss function衡量了单个训练样本的表现，对于m个样本，我们定义Cost function (代价函数) ，它衡量了全体训练样本的表现

$$J(w,b) = \frac{1}{m} \sum_{i=1}^{m}L(\hat{y}^{(i)},y^{(i)}) = -\frac{1}{m} \sum_{i=1}^{m}y^{(i)} \log\hat{y}^{(i)} + (1-y^{(i)}) \log(1-\hat{y}^{(i)})$$

Loss function只适用于单个训练样本，Cost function是基于参数的总代价。所以，在训练对数几率回归模型时，我们要找到合适的参数 $w, b$ 使得Cost function尽可能的小

Gradient Descent

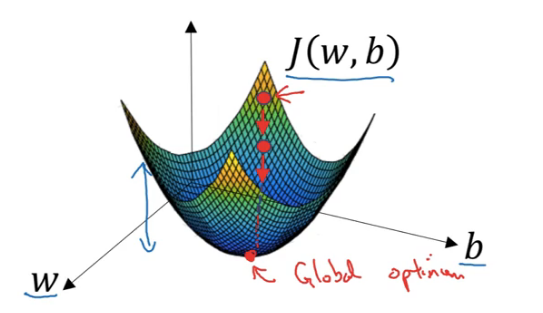
我们将使用梯度下降 (Gradient Descent) 算法来找出合适的参数 $w,b$，使得Cost function 即 $J(w,b)$ 最小

• 

最上方的小红点为初始点，对于对数几率回归，一般使用0来初始化，随机初始化也有效，但通常不这么做

梯度下降过程：

• 从初始点开始，朝最陡的下坡方向走一步
• 重复上述过程，不断修正 $w, b​$ 使得 $J(w,b)​$ 接近全局最优值 (global opitmal)

代码表述为：

Repeat {
$w := w - \alpha \frac{\partial J(w,b)}{\partial w}​$      在代码中 $\frac{\partial J(w,b)}{\partial w}​$ 记作”dw”
$b := b - \alpha \frac{\partial J(w,b)}{\partial b}​$      在代码中 $\frac{\partial J(w,b)}{\partial b}​$ 记作”db”
}

Computation Graph

神经网络的训练包含了两个过程：

• 正向传播 (Forward Propagation)，从输入经过一层层神经网络，最后得到 $\hat{y}$ ，从而计算代价函数 $J$
• 反向传播 (Back Propagation)，根据损失函数 $L(\hat{y},y)$ 来反方向的计算每一层参数的偏导数，从而更新参数

下面我们用计算图 (Computation Graph) 来理解这个过程

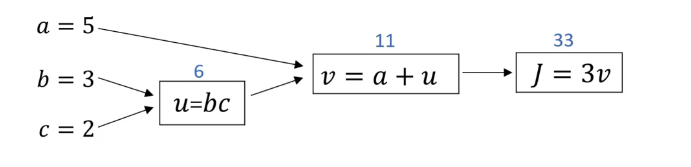
从左向右，可以计算出 $J​$ 的值，对应着神经网络中输入经过计算得到代价函数 $J(w,b)​$ 值的过程

从右向左，根据求导的链式法则，可以得到：

$$\frac{\partial J}{\partial a} = \frac{\partial J}{\partial v} \cdot \frac{\partial v}{\partial a} = 3 \cdot 1 = 3$$ $$\frac{\partial J}{\partial b} = \frac{\partial J}{\partial v} \cdot \frac{\partial v}{\partial u} \cdot \frac{\partial u}{\partial b} = 3 \cdot 1 \cdot c = 6$$ $$\frac{\partial J}{\partial c} = \frac{\partial J}{\partial v} \cdot \frac{\partial v}{\partial u} \cdot \frac{\partial u}{\partial c} = 3 \cdot 1 \cdot b = 9$$

在反向传播中，一般我们只关心最终输出值 (在这个例子中是 $J$ ) ，需要计算 $J$ 对于某个变量 (记作var) 的导数，即 $\frac {dJ}{dvar}​$，在Python代码中简写为dvar

Logistic Regression Gradient Descent

现在，我们来实现对数几率回归梯度下降算法，只考虑单个样本的情况 :

$z = w^{T}x + b$

$\hat{y} = a = \sigma({z})​$

$L(\hat{y},y) = -(y \log\hat{y} + (1-y) \log(1-\hat{y}))​$

假设样本只有两个，分别为 $x1, x2$，则计算图如下 :

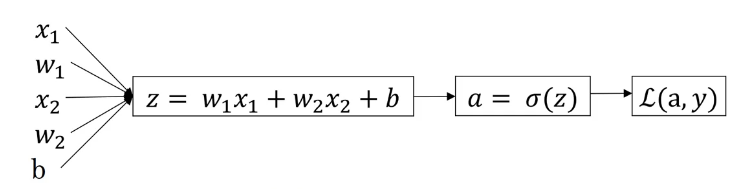
在对数几率回归中，我们需要做的是，改变参数 $w, b$ 的值，来最小化损失函数，即需要计算出 $dw, dz$

向后传播计算损失函数 $L​$ 的偏导数步骤如下：

• $da = \frac {\partial L(a,y)}{\partial a} = -\frac {y}{a} + \frac{1-y}{1-a}​$
• $dz = \frac {\partial L}{\partial z} = \frac {\partial L}{\partial a} \cdot \frac {da}{dz}= (-\frac {y}{a} + \frac{1-y}{1-a}) \cdot a \cdot (1-a) = a - y​$
• $dw_1 = \frac {\partial L}{\partial w_1} = \frac {\partial L}{\partial z} \cdot \frac { \partial z}{\partial w_1} = x_1 \cdot dz ​$
• $dw_2 = \frac {\partial L}{\partial w_2} = \frac {\partial L}{\partial z} \cdot \frac { \partial z}{\partial w_2} = x_2 \cdot dz ​$
• $db = \frac {\partial L}{\partial b} = \frac {\partial L}{\partial z} \cdot \frac { \partial z}{\partial b} = dz​$

所以，在对数几率回归梯度下降算法中你需要做的是

• $ dz = a - y$
• $dw_1 = x_1 \cdot dz ​$
• $dw_2 = x_2 \cdot dz ​$
• $db = dz​$
• 更新$w_1​$, $w_1 = w_1 - \alpha dw_1​$
• 更新$w_2$, $w_2 = w_2 - \alpha dw_2$
• 更新$b​$, $b = b - \alpha db​$

Gradient descent on $m$ examples

之前只实现了单个样本的梯度下降算法，现在我们将梯度下降算法应用到整个训练集

$J(w,b) = \frac{1}{m} \sum_{i=1}^{m}L(\hat{y}^{(i)},y^{(i)}) $

$a^{(i)} = \hat{y}^{(i)} = \sigma(z^{(i)}) = \sigma(w^{T}x^{(i)}+b)​$

$\frac {\partial}{\partial w_1}J(w,b) = \frac {1}{m} \sum_{i=1}^{m} \frac {\partial}{\partial w_1}L(a^{(i)},y^{(i)}) = \frac {1}{m} \sum_{i=1}^{m}dw_1^{(i)}$

• $dw_1^{(i)}​$按照之前单个样本的情况计算

伪代码如下 :

$J=0; dw_1=0; dw_2=0; db=0;$
$for \quad i = 1 \quad to \quad m $
$\quad z^{(i)} = w^{T}x^{(i)}+b$
$\quad a^{(i)} = \sigma(z^{(i)})$
$\quad J += -(y^{(i)} \log a^{(i)} + (1-y^{(i)}) \log(1-a^{(i)}))$
$\quad dz^{(i)} = a^{(i)}-y^{(i)}$
$\quad dw_1 += x_1^{(i)}dz^{(i)}$
$\quad dw_2 += x_2^{(i)}dz^{(i)} \qquad$
$\quad…\quad\quad\quad\quad\quad\quad$ //这里应该是一个循环，这里 $n_x = 2$
$\quad db += dz^{(i)}$
​$J /= m$
$dw_1 /= m$
$dw_2 /= m$
$db /= m$

$w_1 = w_1 - \alpha dw_1​$
$w_2 = w_2 - \alpha dw_2​$
$b = b - \alpha db​$

但这种方法，有两个循环，一个是最外层的循环，循环 $m$ 个训练样本，另一个是 $dw_1, dw_2$ (feature) 的循环，在这个例子中 $n_x = 2$。随着训练集越来越大，应该尽量避免使用for循环，而使用向量化技术 (vectorization)